Difference between revisions of "Creating Bluish Noise With Minimal Compute"
| (14 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | Often random numbers are referred to as "noise", and sometimes we attach colours to refer to the different characteristics of that noise. The colours reference power characteristics at at different frequencies, but those power characteristics are the ultimately the result of how the random values are distributed. | ||
| + | |||
Blue noise is a type of noise with a power density that increases with frequency, giving it a high-pitched, hissy sound. Visually, it manifests as a pattern with minimal low-frequency components and a relatively even distribution of points, and is frequently used for dithering. Blue noise is often used for its aesthetically pleasing randomness, since numbers don't clump together as they would with truly random (white noise) sources. | Blue noise is a type of noise with a power density that increases with frequency, giving it a high-pitched, hissy sound. Visually, it manifests as a pattern with minimal low-frequency components and a relatively even distribution of points, and is frequently used for dithering. Blue noise is often used for its aesthetically pleasing randomness, since numbers don't clump together as they would with truly random (white noise) sources. | ||
| − | == | + | == Saarna's Bluing Algorithm == |
| − | Blue noise is typically created by generating random values, and massaging them in various ways to not be as clumpy. This isn't a great approach for older platforms that don't have a lot of compute or ram. | + | Blue noise is typically created by generating random values, and massaging them in various ways to not be as clumpy. This isn't a great approach for older platforms that don't have a lot of compute horsepower or ram. |
| − | An alternative approach is to | + | An alternative approach, is to blue the noise by keeping track of recent values with an exponentially decaying running average, and ensuring that new random numbers aren't near the decaying average... |
| − | A= | + | A=GetRandom() ; any masking or range-reduction needs to be done here, or else |
| − | B= | + | B=GetRandom() ; it will reintroduce clumpiness into the value distribution |
| − | if | + | if Absolute(B-C) > Absolute(A-C) then A=B |
C=(C+A)/2 ; exponentially decaying running average | C=(C+A)/2 ; exponentially decaying running average | ||
| − | ; | + | ; "A" is holding your next bluish noise value |
| − | The algorithm creates the | + | The algorithm creates the blue noise characteristic +3 dB per octave power increase, and it works equally well with LFSR noise sources. |
| − | + | The algorithm could be modified to produce bluer noise by adding more random values into the comparison. The algorithm as presented produces noise that is strikingly blue, as can be seen in the following Spectral Analysis section, so additional random number steps are probably not worth the additional effort for most applications. | |
| + | |||
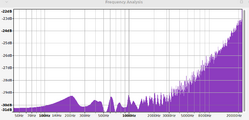
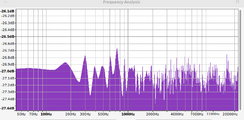
| + | == Spectral Analysis == | ||
| + | <gallery widths=800px> | ||
| + | File:Spectrum_bbblue.png|Spectral Analysis of a 16-bit LFSR after application of the bluing algorithm. | ||
| + | File:Spectrum_bb16.png|Spectral Analysis of a 16-bit LFSR without application of the bluing algorithm. | ||
| + | </gallery> | ||
== Authorship == | == Authorship == | ||
| − | + | The novel algorithm described here was created by Mike Saarna. If you're going to cite, please refer to it as "Saarna's Bluing Algorithm". | |
| − | The novel | ||
Latest revision as of 18:09, 23 May 2024
Often random numbers are referred to as "noise", and sometimes we attach colours to refer to the different characteristics of that noise. The colours reference power characteristics at at different frequencies, but those power characteristics are the ultimately the result of how the random values are distributed.
Blue noise is a type of noise with a power density that increases with frequency, giving it a high-pitched, hissy sound. Visually, it manifests as a pattern with minimal low-frequency components and a relatively even distribution of points, and is frequently used for dithering. Blue noise is often used for its aesthetically pleasing randomness, since numbers don't clump together as they would with truly random (white noise) sources.
Saarna's Bluing Algorithm
Blue noise is typically created by generating random values, and massaging them in various ways to not be as clumpy. This isn't a great approach for older platforms that don't have a lot of compute horsepower or ram.
An alternative approach, is to blue the noise by keeping track of recent values with an exponentially decaying running average, and ensuring that new random numbers aren't near the decaying average...
A=GetRandom() ; any masking or range-reduction needs to be done here, or else B=GetRandom() ; it will reintroduce clumpiness into the value distribution if Absolute(B-C) > Absolute(A-C) then A=B C=(C+A)/2 ; exponentially decaying running average ; "A" is holding your next bluish noise value
The algorithm creates the blue noise characteristic +3 dB per octave power increase, and it works equally well with LFSR noise sources.
The algorithm could be modified to produce bluer noise by adding more random values into the comparison. The algorithm as presented produces noise that is strikingly blue, as can be seen in the following Spectral Analysis section, so additional random number steps are probably not worth the additional effort for most applications.
Spectral Analysis
Spectral Analysis of a 16-bit LFSR after application of the bluing algorithm.
Spectral Analysis of a 16-bit LFSR without application of the bluing algorithm.
Authorship
The novel algorithm described here was created by Mike Saarna. If you're going to cite, please refer to it as "Saarna's Bluing Algorithm".
