Creating Bluish Noise With Minimal Compute

Often random numbers are referred to as "noise", and sometimes we attach colours to refer to the different characteristics of that noise. The colours reference power characteristics at at different frequencies, but those power characteristics are the ultimately the result of how the random values are distributed.

Blue noise is a type of noise with a power density that increases with frequency, giving it a high-pitched, hissy sound. Visually, it manifests as a pattern with minimal low-frequency components and a relatively even distribution of points, and is frequently used for dithering. Blue noise is often used for its aesthetically pleasing randomness, since numbers don't clump together as they would with truly random (white noise) sources.

The Algorithm

Blue noise is typically created by generating random values, and massaging them in various ways to not be as clumpy. This isn't a great approach for older platforms that don't have a lot of compute horsepower or ram.

An alternative approach is to use an exponentially decaying average, to ensure the next new number isn't clumped together with recently returned numbers...

A=RAND
B=RAND
if ABS(B-C) > ABS(A-C) then A=B
C=(C+A)/2 ; exponentially decaying running average
; "A" is holding your next bluish noise value

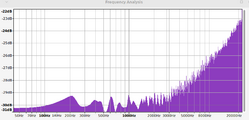
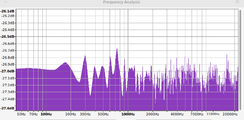
The algorithm creates the expected +3 dB per octave power increase, and works equally well with LFSR noise sources.

Adding more random values into the comparison will purify the blue noise, at the expense of adding more compute time.

Spectrum Analysis

• 

  Spectrum Analysis of a 16-bit LFSR with bluish processing.

• 

  Spectrum Analysis of a 16-bit LFSR without bluish processing.

Authorship

The novel Bluish Noise technique described here was created by Mike Saarna.