Difference between revisions of "The Perceptual Tuning Primer"
(→Theory) |
|||
| (4 intermediate revisions by the same user not shown) | |||
| Line 8: | Line 8: | ||
This section is rather heavy, while using Perceptual Tuning is rather simple in practice. If you find yourself overwhelmed by the theory, feel free to skip ahead to the [[#PracticalApplication|Practical Application]] section. | This section is rather heavy, while using Perceptual Tuning is rather simple in practice. If you find yourself overwhelmed by the theory, feel free to skip ahead to the [[#PracticalApplication|Practical Application]] section. | ||
| − | When a note sounds "off" to a listener, it isn't because the listener hears that the note is 262 Hz rather than 261.626Hz. It's because the frequency of the note sounds off in relation to other notes in the music. If you speed up the playback of a recording of Beethoven's 5th symphony, the pitch of the notes being | + | When a note sounds "off" to a listener, it isn't because the listener hears that the note is 262 Hz rather than 261.626Hz. It's because the frequency of the note sounds off in relation to other notes in the music. If you speed up the playback of a recording of Beethoven's 5th symphony, the pitch of the notes are being shifted upwards, but overall the recording will still sound in tune because the relationships between the notes remain the same. |
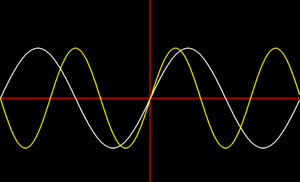
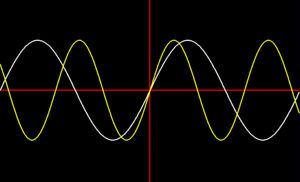
[[File:Frequency and perfect fifth.png|thumb|2 sine waves, a perfect fifth interval apart. Note how one wave beginning quickly lines up with the other. This results in consonance.]] [[File:Frequency and minor sixth.png|thumb|2 sine waves, a minor sixth interval apart. It will be a long while before the waves coincide, which results in dissonance.]] | [[File:Frequency and perfect fifth.png|thumb|2 sine waves, a perfect fifth interval apart. Note how one wave beginning quickly lines up with the other. This results in consonance.]] [[File:Frequency and minor sixth.png|thumb|2 sine waves, a minor sixth interval apart. It will be a long while before the waves coincide, which results in dissonance.]] | ||
| Line 16: | Line 16: | ||
When we play 2 or more notes that are normally consonant on an instrument that is slightly out of tune, waves that should normally align with regular periodicity lose that alignment and take much longer to line up - they become more dissonant. When we play 2 or more notes together that are normally dissonant on the same out-of-tune instrument, the result is still dissonance. Since our brains use consonance as part of the note identification strategy<ref>[http://www.jneurosci.org/content/29/42/13165.full The Journal of Neuroscience, 21 October 2009, 29(42): 13165-13171; doi: 10.1523/JNEUROSCI.3900-09.2009]</ref>, our ability to detect a poorly tuned instrument is stronger with note relationships that are normally consonant, and weaker with note relationships that are normally dissonant. | When we play 2 or more notes that are normally consonant on an instrument that is slightly out of tune, waves that should normally align with regular periodicity lose that alignment and take much longer to line up - they become more dissonant. When we play 2 or more notes together that are normally dissonant on the same out-of-tune instrument, the result is still dissonance. Since our brains use consonance as part of the note identification strategy<ref>[http://www.jneurosci.org/content/29/42/13165.full The Journal of Neuroscience, 21 October 2009, 29(42): 13165-13171; doi: 10.1523/JNEUROSCI.3900-09.2009]</ref>, our ability to detect a poorly tuned instrument is stronger with note relationships that are normally consonant, and weaker with note relationships that are normally dissonant. | ||
| − | The last bit of theory we need to understand is that almost all music is written in a particular key, which can be thought of as a foundation note by which other notes are measured. The notes played in the song are interpreted by our brains in relation to the key. As notes are played that are dissonant in relation to the key, tension builds. When | + | The last bit of theory we need to understand is that almost all music is written in a particular key, which can be thought of as a foundation note by which other notes are measured. The notes played in the song are interpreted by our brains in relation to the key. As notes are played that are dissonant in relation to the key, tension builds. When notes that are consonant to the key are played, tension is relaxed. |
While TIA is incapable of creating music that is in absolutely in tune, it turns out we can pick a key for creating TIA music that will ensure that the consonant notes are closer to being in tune, while worrying less about the dissonant notes. This is the idea behind Perceptual Tuning. | While TIA is incapable of creating music that is in absolutely in tune, it turns out we can pick a key for creating TIA music that will ensure that the consonant notes are closer to being in tune, while worrying less about the dissonant notes. This is the idea behind Perceptual Tuning. | ||
| Line 26: | Line 26: | ||
==Practical Application== | ==Practical Application== | ||
<div id="PracticalApplication"></div> | <div id="PracticalApplication"></div> | ||
| − | The musical key with the best TIA Perceptual Tuning for any 12 consecutive notes is A3@218.3Hz, and the | + | The musical key with the best TIA Perceptual Tuning score for any 12 consecutive notes is A3@218.3Hz, and the A4 above it is good as well if you can avoid the major third at C#5@561.4Hz. |
| − | + | When you use the key of A3 in your composition, you don't have to avoid the less-well tuned notes - the point of of this technique is we've hidden TIA's weaknesses where our ears are weaker. Just go ahead and write your songs in the key of A3 as if TIA was as perfectly in-tune, and you'll be taking advantage of Perceptual Tuning. | |
==Samples== | ==Samples== | ||
Listen to the samples below to hear the difference between regular tuning, tune2600 selected tuning, and perceptual tuning. The samples contain some worst case examples - familiar songs with sustained notes, and ranges that cover over an octave. | Listen to the samples below to hear the difference between regular tuning, tune2600 selected tuning, and perceptual tuning. The samples contain some worst case examples - familiar songs with sustained notes, and ranges that cover over an octave. | ||
| − | ===O Tannenbaum, in | + | ===O Tannenbaum, in G4=== |
[[File:Tannenbaum - d4.mp3]] | [[File:Tannenbaum - d4.mp3]] | ||
| − | ===O Tannenbaum, in | + | ===O Tannenbaum, in F3 frequencies as selected by tune2600=== |
[[File:Tannenbaum - c3 tune2600.mp3]] | [[File:Tannenbaum - c3 tune2600.mp3]] | ||
===O Tannenbaum, in A3 for Perceptual Tuning=== | ===O Tannenbaum, in A3 for Perceptual Tuning=== | ||
[[File:Tannenbaum - a3 perceptual tuning.mp3]] | [[File:Tannenbaum - a3 perceptual tuning.mp3]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
===Salvo homebrew theme, in A3 for Perceptual Tuning=== | ===Salvo homebrew theme, in A3 for Perceptual Tuning=== | ||
Latest revision as of 03:58, 27 September 2018
Contents
Overview
Perceptual Tuning refers to arranging TIA music in the key of A (specifically A3) with the intent to shift any poorly tuned notes to ones to ones aren't as easily detected as being poorly tuned.
Perceptual Tuning differs from using the Tune2600 utility. Tune2600 will transpose your selected notes to make them as in-tune as possible, with the algorithm considering your selected notes as having equal importance.
Theory
This section is rather heavy, while using Perceptual Tuning is rather simple in practice. If you find yourself overwhelmed by the theory, feel free to skip ahead to the Practical Application section.
When a note sounds "off" to a listener, it isn't because the listener hears that the note is 262 Hz rather than 261.626Hz. It's because the frequency of the note sounds off in relation to other notes in the music. If you speed up the playback of a recording of Beethoven's 5th symphony, the pitch of the notes are being shifted upwards, but overall the recording will still sound in tune because the relationships between the notes remain the same.
Some note relationships differ in quality from others. When 2 or more note frequencies line up with simple and short periodicity, our brains detect that. There's even have a musical name for it - it's called consonance[1]. When the frequencies don't line up regularly, its called dissonance[1].
When we play 2 or more notes that are normally consonant on an instrument that is slightly out of tune, waves that should normally align with regular periodicity lose that alignment and take much longer to line up - they become more dissonant. When we play 2 or more notes together that are normally dissonant on the same out-of-tune instrument, the result is still dissonance. Since our brains use consonance as part of the note identification strategy[2], our ability to detect a poorly tuned instrument is stronger with note relationships that are normally consonant, and weaker with note relationships that are normally dissonant.
The last bit of theory we need to understand is that almost all music is written in a particular key, which can be thought of as a foundation note by which other notes are measured. The notes played in the song are interpreted by our brains in relation to the key. As notes are played that are dissonant in relation to the key, tension builds. When notes that are consonant to the key are played, tension is relaxed.
While TIA is incapable of creating music that is in absolutely in tune, it turns out we can pick a key for creating TIA music that will ensure that the consonant notes are closer to being in tune, while worrying less about the dissonant notes. This is the idea behind Perceptual Tuning.
To find the key that had the best TIA Perceptual Tuning properties, a program was created that ran through all of the available frequencies and scored them according to how in-tune the following notes were. The score for any given note was weighted according to the relationship of the note to it's key, with much larger weights being assigned to relationships with strong consonance - the major third, perfect fourth, perfect fifth, and octave intervals.
The program found that A3@218.3Hz has the best Perceptual Tuning score, with the first 12 semitones having good perceptual tuning, with the next 12 semitones being decent except for an out-of-tune major third at C#5@561.4Hz.
Practical Application
The musical key with the best TIA Perceptual Tuning score for any 12 consecutive notes is A3@218.3Hz, and the A4 above it is good as well if you can avoid the major third at C#5@561.4Hz.
When you use the key of A3 in your composition, you don't have to avoid the less-well tuned notes - the point of of this technique is we've hidden TIA's weaknesses where our ears are weaker. Just go ahead and write your songs in the key of A3 as if TIA was as perfectly in-tune, and you'll be taking advantage of Perceptual Tuning.
Samples
Listen to the samples below to hear the difference between regular tuning, tune2600 selected tuning, and perceptual tuning. The samples contain some worst case examples - familiar songs with sustained notes, and ranges that cover over an octave.
O Tannenbaum, in G4

O Tannenbaum, in F3 frequencies as selected by tune2600

O Tannenbaum, in A3 for Perceptual Tuning

Salvo homebrew theme, in A3 for Perceptual Tuning

Limitations
Perceptual Tuning by definition uses the A3 key for composition, so it isn't possible to use it with music that incorporates key changes.
While playing 2-note chords is possible with TIA and Perceptual Tuning, it should be noted that the chord-note relationships aren't necessarily covered by Perceptual Tuning. The relationship between the notes in the chord will result in consonance/dissonance relative to those notes, in addition to the consonance/dissonance between the key and notes played. Because of this some chords may sound out of tune, even if individual notes sound fine. Care and experimentation is recommended when using chords.
Utility Source Code
The program identified A3 as the strongest match, and will do so every time. However the source code is provided here for those who might wish to validate, tinker, or adapt. Consider this source Public Domain. The author accepts no liability resulting from the program's use, and offers no warranty.
Authorship
The Perceptual Tuning Primer was written by Mike Saarna (aka RevEng) as original content for 7800.8bitdev.org.
References
- ↑ 1.0 1.1 https://en.wikipedia.org/wiki/Consonance_and_dissonance
- ↑ The Journal of Neuroscience, 21 October 2009, 29(42): 13165-13171; doi: 10.1523/JNEUROSCI.3900-09.2009